一、报告题目：Validity of a new continuum model for the evolution of grain boundaries in polycrystalline materials

二、报告人：朱佩成 教授

三、时  间：2025年11月21日（周五）15:00-16:00

四、地 点：闻理园A4-305

报告摘要：A continuum equation was proposed by Zhang, et al to model the motion of grain boundaries based on the underlying microscopic mechanisms of line defects (disconnections) and the integrated effects of a diverse range of thermodynamic driving forces. The model reads

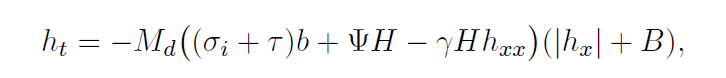
where the unknown function h is the height of grain boundary from reference line, \sigma_i is the stress due to the elastic interaction between disconnections based on their dislocation nature, defined by

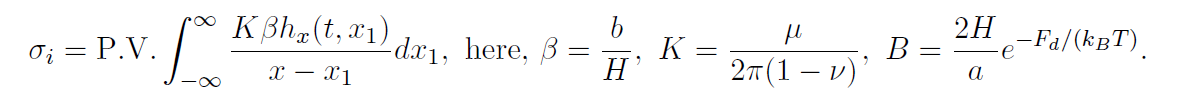
Here P.V. denotes the Cauchy principal value, M_d, \tau, b, \psi, H, \gamma, F_d, a, k_B, T are, respectively, the mobility constant, the applied stress, the Burgers vector, the energy jump across the GB, step height of a disconnection, the GB energy, the disconnection formation energy, the lattice constant, the Boltzmann constant, the temperature. And B is associated with the equilibrium density of the disconnection pairs. Finally \mu, \nu are standard notations for the shear modulus and Poisson ratio, respectively.

We study the validity of this model from the aspects of well-posedness and numerical experiments, of an initial-(periodic-) boundary value problem (IBVP) for this model, and prove the global existence, uniqueness, and regularity of weak solution to this IBVP. Also we show that the stationary solution exists. We finally investigate the large-time behavior of the solution, which is shown that the solution converges to the steady state in a suitable sense, and numerical simulations are carried out to justify this. The main difficulties in the proof of main theorems are due to a non-local term with singularity, and a non-smooth coefficient of the highest derivative associated with the gradient of the unknown. The key ingredients in the proof are the energy method, an estimate for a singular integral of the Hilbert type, and Fourier transform of Hilbert transformations.

报告人简介：朱佩成，上海大学教授，入选上海高端人才计划，在多个国家任过职，并在欧洲取得永久职位。在 CPM, ARMA, M3AS,  SIAM J. Appl. Math., Proc. Roy. Soc. Edinburgh Sect. A， J. Differential Equations 国际杂志发表了60多篇论文。

欢迎广大师生参加！联系人：非线性偏微分方程团队 边行之